A bit of theory...

Dielectrophoresis principle

The term "dielectrophoresis" was first introduced by Pohl in 19511 to describe the motion of dielectric particles due to interaction with a non uniform electric field.

Depending on the frequency of the applied field and on the dielectric properties of the particle and its immersion medium, different polarization mechanisms come into play, the main mechanisms being related to the formation of a double electric layer at the particle/liquid interface and to charge accumulation at interfaces between media of different electrical properties (Maxwell-Wagner interfacial polarization effect)2.

The force resulting from the interaction between the induced dipole moment $\mathbf{m}$ and the field gradient is expressed by: $$\begin{equation} \mathbf{F_{DEP}}=-\mathbf \nabla U_{El}=(\mathbf m.\mathbf \nabla)\mathbf E \tag{1} \label{FDEP} \end{equation}$$ where $U_{El}$ refers to the electric potential energy and $\mathbf E$ to the electric field.

For a spherical particle of radius $r_{ext}$, the induced dipolar moment is given by: $$\mathbf{m}=4\pi \varepsilon_{m} \varepsilon_{0} CM(f) r_{ext}^3 \mathbf {E} \tag{2} \label{eqm} $$

where $CM(f)$ is the Clausius-Mossotti factor: \begin{equation} CM(f)=\frac{\varepsilon_{p}^{\ast}-\varepsilon_{m}^{\ast}}{\varepsilon_{p}^{\ast}+2\varepsilon_{m}^{\ast}} \tag{3} \label{eqCM} \end{equation} $\varepsilon_{p}^{\ast}$ and $\varepsilon_{m}^{\ast}$ refer to the complex permittivities of particle and medium, which depend on their respective conductivities and permittivities and on the field angular frequency $\omega$ : \begin{equation} \varepsilon_i^{\ast}= \varepsilon_{i}\varepsilon_{0}-j\frac{\sigma_i}{\omega} \tag{4} \label{eps_c} \end{equation}

where $\varepsilon_{i}$ is the relative permittivity, $\varepsilon_{0}$ the vacuum permittivity and $\sigma_i$ the electrical conductivity.

Development of equation \eqref{FDEP} leads to the expression of the generalized DEP force3: $$\begin{equation} \mathbf{F_{DEP}}=2\pi \varepsilon_{m} \varepsilon_{0} r_{ext}^3 \left\{ Re[CM(f)]\mathbf \nabla E_{RMS}^2+Im[CM(f)] (E_x^2\mathbf \nabla \phi_x+E_y^2\mathbf \nabla \phi_y+E_z^2\mathbf \nabla \phi_z) \right\} \tag{5}\label{FDEP_full} \end{equation}$$

Conventional dielectrophoresis

When a stationary field is applied, the expression of the time-averaged DEP force \eqref{FDEP_full} simplifies to: $$\mathbf{F_{cDEP}}=2\pi \varepsilon_{m} \varepsilon_{0} r_{ext}^3 Re[CM(f)]\mathbf \nabla E_{RMS}^2 \tag{6} \label{FcDEP}$$ This phenomenon is sometimes referred to as "conventional dielectrophoresis" (cDEP). The force depends on the gradient of the squared electric field intensity and exists only in the presence of a non uniform electric field. It is proportional to the volume of the particle, as well as to the real part of the Clausius-Mossotti factor, $ Re[CM(f)] $. This term reflecting the polarizability contrast between the particle and its immersion medium also determines the direction of the force:

Fig.1 Illustration of pDEP principle. A. The particle and its immersion medium get polarized under the effect of the electric field. Here the particle is more polarizable than its immersion medium. B. The net dipole moment $\mathbf m$ is directed in the same direction as the field. Due to the field non uniformity ($E_B>E_A$), coulomb forces exerted on opposed induced charges are unbalanced ($F_B>F_A$), which induces a net displacement of the particle towards the region of maximum field intensity.

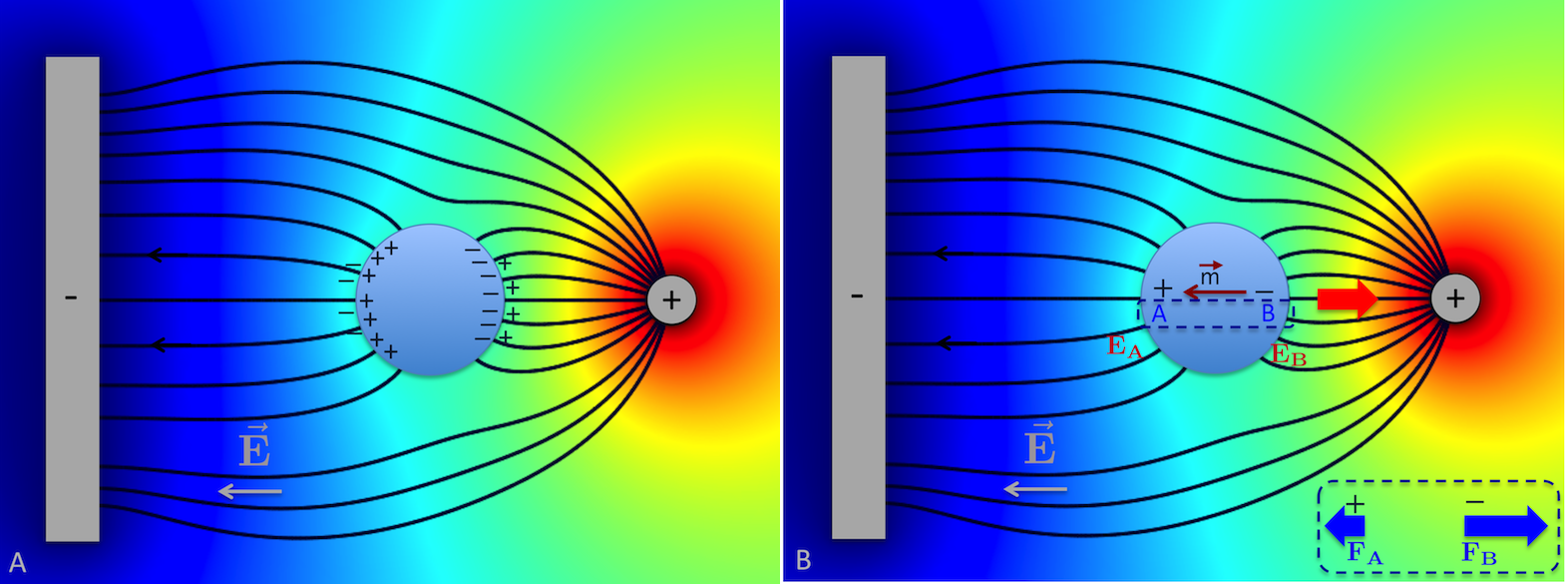
Electrorotation

While conventional dielectrophoresis is based on the use of stationary electric fields, electrorotation consists in inducing a rotary motion on a polarizable particle exposed to a rotating field. This technique was developed in the 1980s by Arnold and Zimmermann4, who proposed to use a four-pole electrode structure to generate the field by applying 90° phase-shifted signals between two adjacent electrodes.

When a polarizable particle is suspended in a rotating electric field, a dipole forms and should rotate synchronously with the field. In practice, when the angular frequency of the field is sufficiently high, the dipolar relaxation time is too long to allow this synchronism. The temporal shift (or phase delay) resulting between the dipole and the field results in a torque exerted on the particle, of expression: $$\langle\mathbf{\Gamma_{EL}}\rangle=\mathbf{m}\times\mathbf{E}=-4\pi r_{ext}^{3}\varepsilon_{m}\varepsilon_{0}Im[CM(f)]E^{2}\mathbf{e_z} \tag{7} \label{ROT_torque}$$ where $\mathbf{e_z}$ represents the unit vector normal to the electrode plane and $CM(f)$ the Clausius-Mossotti factor. (cf \eqref{eqCM}).

At the equilibrium between induced torque and viscous drag, the rotation rate for a spherical particle is given by: $$\Omega(\omega)=-\frac{\varepsilon_{0}\varepsilon_{m}}{2\eta}Im[CM(f)]E^{2} \tag{8} \label{Omega}$$ where $\eta$ represents the medium viscosity.

The minus sign indicates that the particle rotates against the field direction for $Im[CM(f)]>0$. Otherwise the direction of rotation is with the field. Curve fitting procedures may be used to obtain the dielectric parameters of a cell, by minimizing the deviation between the experimental ROT spectrum (plot of the rotation rate with respect to the field frequency) and the theoretical spectrum predicted by the appropriate multi-shell model.

Travelling-wave dielectrophoresis (twDEP)

The twDEP force acts on a particle subjected to a travelling electric field. It is related to the phase non-uniformity of the electric field and arises from the interaction of the travelling field with the phase lagging component of the induced dipole moment. Such a field can be produced by planar electrodes arranged in rows and driven by a polyphase ac voltage. twDEP is therefore an analogue of ROT, with electrodes arranged in line, rather than in a circle. The resulting translational force propels the particle along the electrodes, with or against the field direction, depending on whether $Im[CM(f)]$ is negative or positive, respectively. In practice, cDEP and twDEP effects can be observed simultaneously: while the particle translates, it is either pushed above the electrodes (nDEP) or attracted onto them (pDEP), depending on the sign of $Re[CM(f)]$5.

Cell modelling

Most particles, and especially biological cells, are not homogeneous. It is therefore mandatory to model the different layers that constitute them (cell membrane and cytoplasm in particular). Calculating the Clausius-Mossotti factor requires to successively calculate the equivalent permittivities of the inner layers to obtain an homogeneous equivalent particle. The different models implemented in MyDEP are: "Homogeneous particle", "Single-shell", "Two-shell", "Three-shell" and "Four-shell" and are presented in Fig.2.

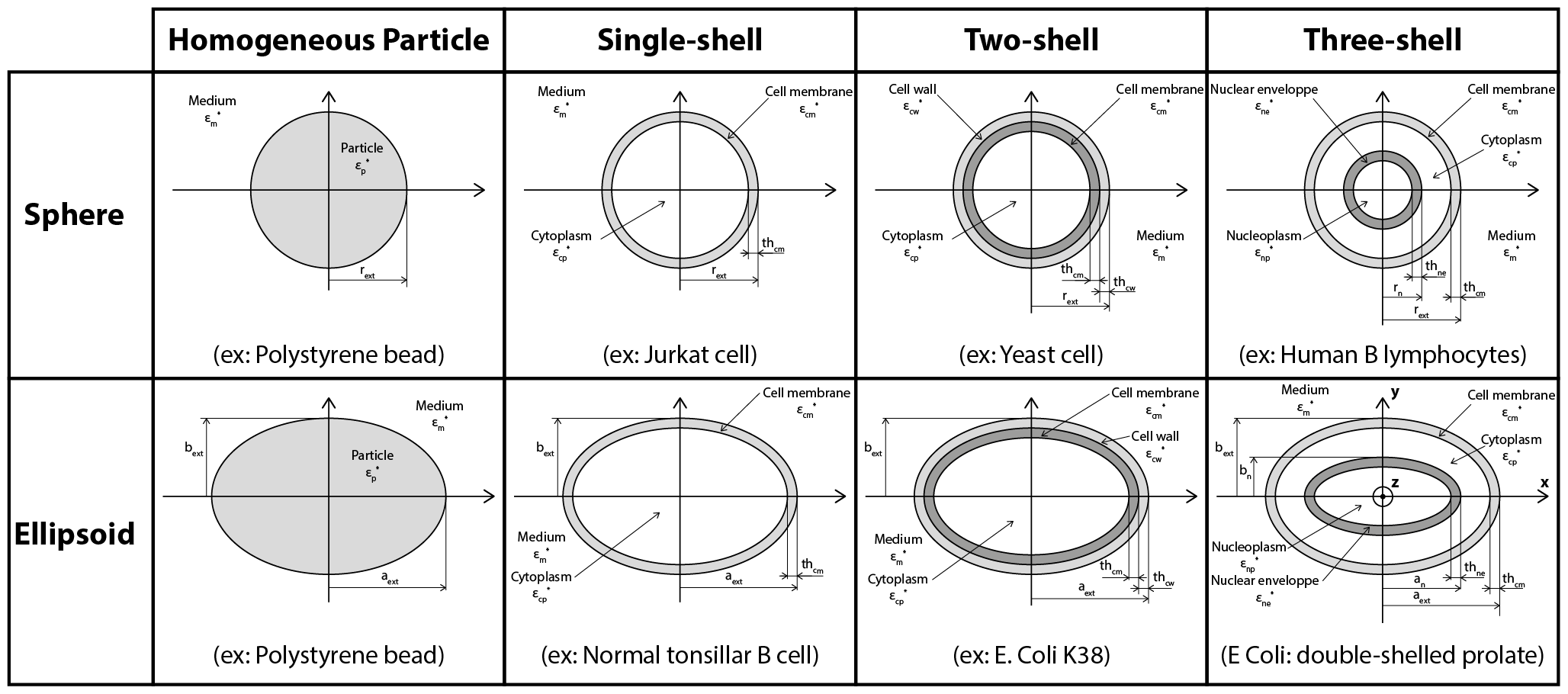
Fig.2 Illustration of the different spherical and ellipsoidal cell and particle models implemented in the interface. All the models "Homogeneous sphere", "Single-shell", "Two-shell" and "Three-shell" are illustrated with an example. The implemented "Four-shell" model is not illustrated here.

For a cell modelled with a "Single-shell" model composed of a cytoplasm surrounded by a cell membrane, the equivalent complex permittivity6 is: \begin{equation} \tag{9} \epsilon_{eq}^{\ast}=\epsilon_{cm}^{\ast}\frac{\left(\frac{r_{ext}}{r_{ext}-th_{cm}}\right)^3+2\left(\frac{\epsilon_{cp}^{\ast}-\epsilon_{cm}^{\ast}}{\epsilon_{cp}^{\ast}+2\epsilon_{cm}^{\ast}}\right)}{\left(\frac{r_{ext}}{r_{ext}-th_{cm}}\right)^3-\left(\frac{\epsilon_{cp}^{\ast}-\epsilon_{cm}^{\ast}}{\epsilon_{cp}^{\ast}+2\epsilon_{cm}^{\ast}}\right)} \end{equation} The formulation of the complex permittivity for ellipsoids has been described by Kakutani et al.7.

Cell suspension

In the presence of particles, the effective permittivity of the suspension $\epsilon_{mix}^{\ast}$ depends on the volume fraction $\phi$ occupied by the particles. It is given by the Maxwell-Garnett mixing equation if the volume fraction $\phi < 0.1$

\begin{equation} \tag{10} \frac{\epsilon_{mix}^{\ast}-\epsilon_{m}^{\ast}}{\epsilon_{mix}^{\ast}+2\epsilon_{m}^{\ast}}=\phi\frac{\epsilon_{p}^{\ast}-\epsilon_{m}^{\ast}}{\epsilon_{p}^{\ast}+2\epsilon_{m}^{\ast}} \end{equation}

which is equivalent, according to Sihvola et al.8, to the direct formulation:

\begin{equation} \tag{11} \epsilon_{mix}^{\ast}=\epsilon_{m}^{\ast} \left(1+3 \phi \frac{\frac{\epsilon_{p}^{\ast}-\epsilon_{m}^{\ast}}{\epsilon_{p}^{\ast}+2\epsilon_{m}^{\ast}}}{1-\phi\frac{\epsilon_{p}^{\ast}-\epsilon_{m}^{\ast}}{\epsilon_{p}^{\ast}+2\epsilon_{m}^{\ast}}}\right) \end{equation}

or by the Asami-Hainaï equation9, theoretically up to $\phi < 0.9$:

\begin{equation} \tag{12} \left(\frac{\epsilon_{mix}^{\ast}-\epsilon_{p}^{\ast}}{\epsilon_{m}^{\ast}-\epsilon_{p}^{\ast}}\right)\left(\frac{\epsilon_{m}^{\ast}}{\epsilon_{p}^{\ast}}\right)^{1/3}=1-\phi \end{equation}

Unfortunately there is no direct expression for the calculation of $\epsilon_{mix}^{\ast}$ and the value can therefore be obtained either by solving the cubic equation or by numerical integration with the difference equation of Hanai's equation. The later has been implemented in the software, with the possibility to choose the number of increments. The full methodology can be found in the papers from Hanai et al.10,11.

References

  1. Pohl, H. A. The Motion and Precipitation of Suspensoids in Divergent Electric Fields. Journal of Applied Physics 22, 869-871, 1951 doi:10.1063/1.1700065
  2. Pethig, R. R. Dielectrophoresis: Theory, methodology and biological applications. John Wiley & Sons, 2017 doi:10.1002/9781118671443
  3. Hughes, M. P. Nanoelectromechanics in engineering and biology. CRC, 2002 url:http://epubs.surrey.ac.uk/id/eprint/836964
  4. Arnold, W. M. & Zimmermann, U. Electro-Rotation - Development of a Technique for Dielectric Measurements on Individual Cells and Particles. Journal of Electrostatics 21, 151-191, 1988 doi:10.1016/0304-3886(88)90027-7
  5. Jones, T. B. Basic theory of dielectrophoresis and electrorotation. Ieee Engineering in Medicine and Biology Magazine 22, 33-42, 2003 doi:10.1109/memb.2003.1304999
  6. Gascoyne, P. R. C., Becker, F. F. & Wang, X. B. Numerical-Analysis of the Influence of Experimental Conditions on the Accuracy of Dielectric Parameters Derived from Electrorotation Measurements. Bioelectrochemistry and Bioenergetics 36, 115-125, 1995 doi:10.1016/0302-4598(94)05015-M
  7. Kakutani, T., Shibatani, S. & Sugai, M. Electrorotation of non-spherical cells: Theory for ellipsoidal cells with an arbitrary number of shells. Bioelectrochemistry and Bioenergetics 31, 131-145, 1993 doi:10.1016/0302-4598(93)80002-c
  8. Sihvola, A. H. & Kong, J. A. Effective permittivity of dielectric mixtures. IEEE Transactions on Geoscience and Remote Sensing 26, 420-429, 1988 doi:10.1109/36.3045
  9. Hanai, T. Theory of the dielectric dispersion due to the interfacial polarization and its application to emulsions. Kolloid-Zeitschrift 171, 23-31, 1960 doi:10.1007/bf01520320
  10. Hanai, T., Asami, K. & Koizumi, N. Dielectric theory of concentrated suspension of shell-spheres in particular reference to the analysis of biological cell suspensions. Bulletin of the Institute for Chemical Research, Kyoto University 57, 297-305, 1979 http://hdl.handle.net/2433/76842
  11. Irimajiri, A., Suzaki, T., Asami, K. & Hanai, T. Dielectric modeling of biological cells. Models and algorithm. Bull. Inst. Chem. Res., Kyoto University 69, 421-438, 1991 http://hdl.handle.net/2433/77400


Back to top